数据结构之【数组】

概念与原理

数组（Array）是一种线性表数据结构，它用一组连续的内存空间，来存储一组具有相同类型的数据。数组可以分为静态数组和动态数组两大类。

静态数组：是一块连续的内存空间，我们可以通过索引来访问这块内存空间中的元素，这也是数组的原始形态。
动态数组：是编程语言为了方便开发者使用，在静态数组的基础上添加了一些常用的API，如push, insert, remove 等方法,这些API可以让我们更方便的操作数组元素，不用自己写代码去实现。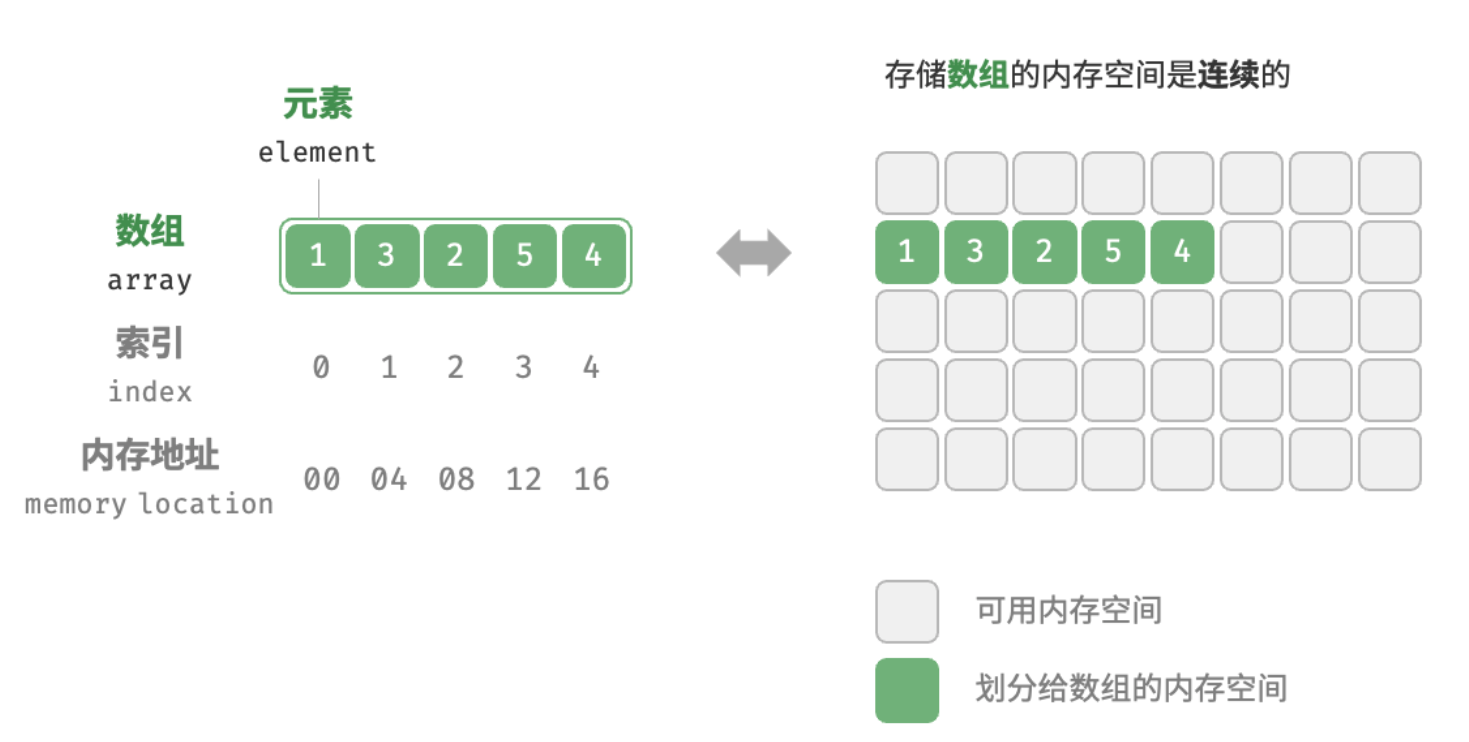

数组的常用操作（增删改查）

数据结构的职责就是增删改查，再无其他。

数组的特性

适合查询多修改少的操作，在使用时需要警惕数据访问越界的问题。。

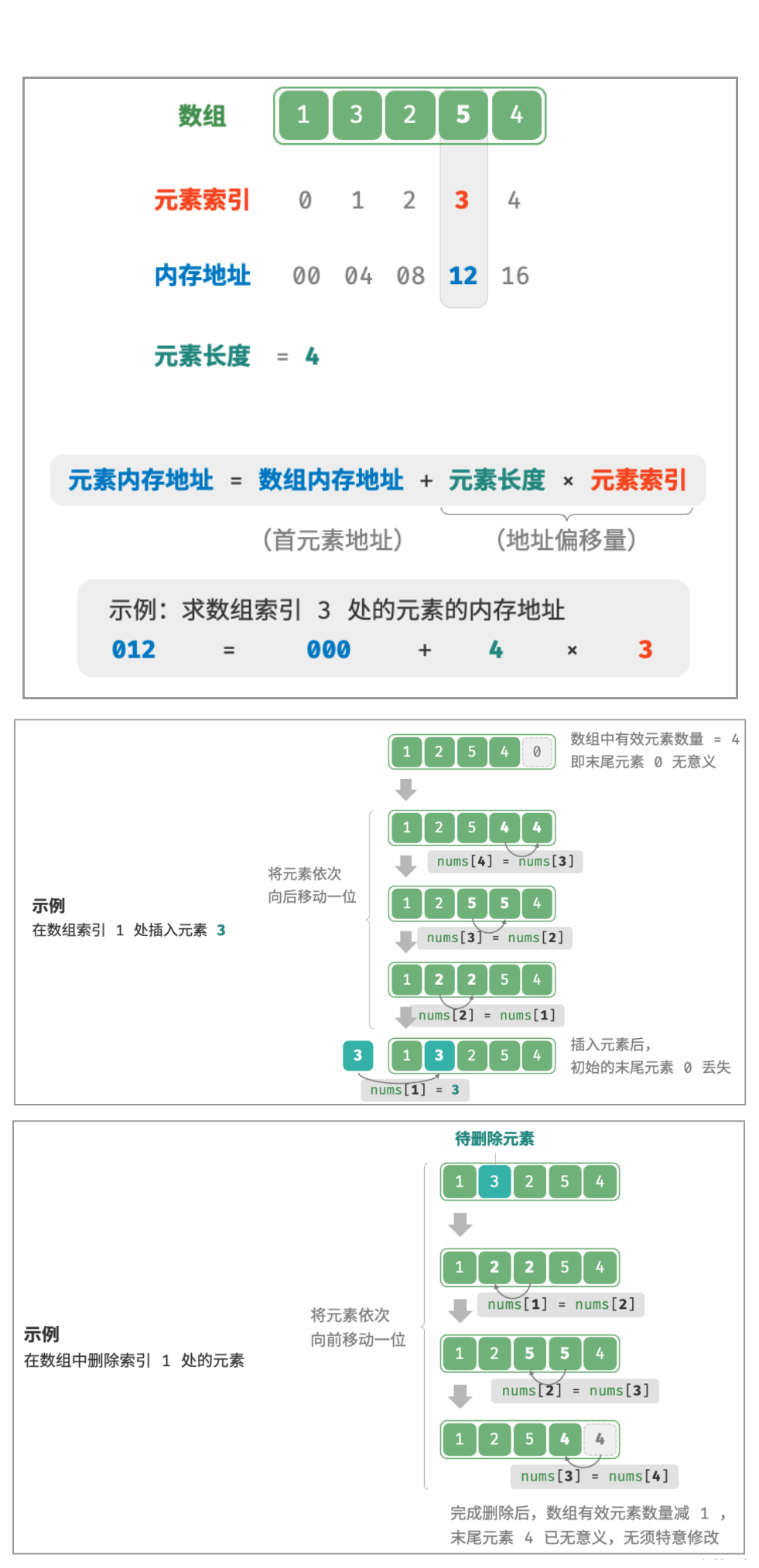
查询效率快，因为数组的结构特点是，根据偏移量（下标）访问速度快，所以随机访问性好。
插入、删除效率低，由于其是连续的线性结构，在删除和插入时通常都会伴随着数据的搬迁。

数组的时间复杂度

在考虑性能时，通常需要去分析不同API的复杂度；另外，数组和链表通常起到了互补的作用，来应对不同的数据处理场景。数组适合查询，链表适合插入和删除。以下列出了常规情况下不同的API的时间复杂度，但具体问题还需要具体分析。

查询(Access)：
- 根据下标随机访问的时间复杂度：O(1)
插入(Insert)：
- 最好情况（末尾插入）时间复杂度：O(1)
- 最坏情况（头部插入）时间复杂度：O(n)
- 平均情况时间复杂度：(1+2+…n)/n = O(n)
删除(Delete)：
- 最好情况（末尾删除）时间复杂度：O(1)
- 最坏情况（开头删除）时间复杂度：O(n)
- 平均情况时间复杂度：O(n)
修改(Update)：
- 给定指定索引，修改索引对应的元素的值，时间复杂度O(1)。

数组典型应用

随机访问：如果想随机抽取一些样本，那么可以用数组存储，并生成一个随机序列，根据索引实现随机抽样。
排序和搜索：数组是排序和搜索算法最常用的数据结构。快速排序、归并排序、二分查找等都主要在数组上进行。
查找表：当需要快速查找一个元素或其对应关系时，可以使用数组作为查找表。假如我们想实现字符到 ASCII 码的映射，则可以将字符的 ASCII 码值作为索引，对应的元素存放在数组中的对应位置。
机器学习：神经网络中大量使用了向量、矩阵、张量之间的线性代数运算，这些数据都是以数组的形式构建的。数组是神经网络编程中最常使用的数据结构。
数据结构实现：数组可以用于实现栈、队列、哈希表、堆、图等数据结构。例如，图的邻接矩阵表示实际上是一个二维数组。

实践应用

实践一：插入操作优化

在数组的k个位置插入一个数据，若不涉及排序操作，只被用来存储数据的集合，比较优选的方案是，将第k个位置的数据移动到数据的末尾，再将需要的数据插入到第k位，这样就避免了其他数据的移动，从而提高了插入效率，且时间复杂度被降到O(1).
快排的实现思路就是如此。

实践二：删除操作优化

通常情况下，删除第k个位置的数据，为了内存的连续性，k后面的数据都需要向前搬迁。
但在不考虑数据的连续性的场景中，则可以将多次删除操作集中在一起操作，从而提升删除效率。具体的做法就是：将需要删除的元素进行标记，并不执行真正的删除操作，当数据没有了更多存储空间时，再触发一次真正的删除操作，这样就能减少因为数据搬迁的次数。
JVM的标记清除垃圾回收算法就是此思想。

实践三：高级编程语言中封装的容器能否替代数组？

如：python中的List， java中的ArrayList、C++中vector等；
通常需要根据实际情况来考虑，通常的关注点是性能方面的，比如说：

若不是特别关注性能，使用编程语言中封装的对象即可，因为这些容器封装了常用操作，牺牲了性能，但让使用变得简单，可用于日常的业务开发
若特别关注性能，建议使用原生数组，因为原生性能好，但使用起来相对比较繁琐，一般用于底层框架的开发，如网络库的开发

相关算法题

数组题目的解法技巧->双指针技巧

在数组中没有真正意义上的指针，通常把索引当做数组中的指针，

左右指针：两个指针相向而行或者相背而行；
快慢指针：两个指针同向而行，一快一慢；

技巧一、快慢指针

应用场景：

应用在【原地修改数组】类型的算法题目上
应用在【滑动窗口】类型的算法题目上
实践思路；
让慢指针走在后面，快指针走在前面探路，在根据题目中的要求，写出相关判断条件。
对于滑动窗口的类型而言：慢指针在后，快指针在前，两个指针中间的部分就是【窗口】，算法通过扩大或缩小窗口来解决相关问题。

# 框架Demo
def demo(nums: List[int], val: int) -> int:
    fast, slow = 0, 0
    while fast < len(nums):
        if nums[fast] != val:
            nums[slow] = nums[fast]
            slow += 1
        fast += 1
    return slow

技巧二、左右指针

常用算法: 二分查找

# 框架Demo
def binary_search(nums: List[int], target: int) -> int:
    # 一左一右两个指针相向而行
    left = 0
    right = len(nums)-1
    while left <= right:
        mid = (right + left) // 2
        if nums[mid] == target:
            return mid 
        elif nums[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1